Destacado

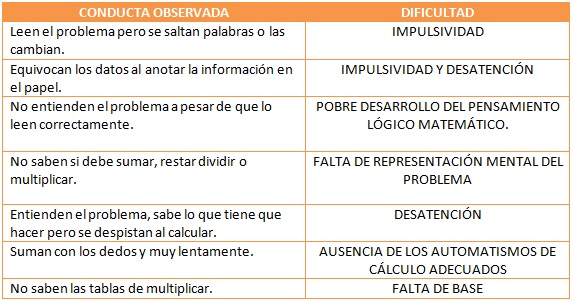
Niños que leen el problema pero se saltan palabras o las cambian para dar sentido a algo que no comprenden: Este es un problema frecuente en los niños hiperactivos. Por lo general, proceden de forma impulsiva leyendo toda la información de una vez, sin analizarla a medida que la descifran. Comenzaremos por el entrenamiento en descifrar instrucciones escritas. Esto frenará su impulsividad y contribuirá a que puedan anotar los datos a medida que descifran el enunciado. Luego aplicaremos estas estrategias a los problemas de matemáticas enseñándoles a representar, a medida que van descifrando el enunciado, los datos del problema mediante un dibujo.

                  

Niños que equivocan los datos al anotar la información en el papel: Éste es un problema que suele ir ligado al anterior. En este caso, los niños son lo suficientemente reflexivos como para leer correctamente el enunciado, pero siguen haciéndolo de corrido, sin detenerse a analizar lo que tratan de procesar. Estos niños manipulan los datos que recuerdan y los combinan en un intento de darles sentido. Por este motivo, equivocan con frecuencia la información que se agolpa sin sentido en su cabeza. Se empieza por el entrenamiento en descifrar instrucciones escritas para pasar luego al entrenamiento en autoinstrucciones, con el fin de enseñarle a organizar y comprender la información.

Niños que no entiende el problema a pesar de que lo leen correctamente: En ocasiones, podemos observar que un niño utiliza las estrategias del entrenamiento en descifrar instrucciones escritas (lee despacio y va anotando la información a medida que aparece) y aun así, no comprende nada. Puede suceder que su pensamiento sea poco abstracto, demasiado concreto, que tenga cierta dificultad para representar mentalmente la información que se deduce de los enunciados. Para comprenderlos necesitan poder palpar la información, es por ello que es conveniente representar los problemas de matemáticas con un dibujo, una interrogante a lo que me piden, pensar en qué operación utilizar, si no imaginar cómo lo haríamos en la vida real y pensar si el resultado tiene sentido.

Niños que no saben si deben sumar, restar dividir o multiplicar: Para ello asociamos el signo a la operación a través de un pequeño juego que les ayude a asociar cada operación: sumar (poner cosas), restar (sacar cosas), multiplicar (poner cosas muchas veces), dividir (repartir cosas). Utilizamos el juego "poner y quitar" para asociarlo: utilizamos una cartulina con cuadrícula y en 1ª fila se dibuja un punto negro. Se trata de poner o quitar fichas del cartón según indiquen los dados y gana el primero que complete su cartón. El objetivo es automatizar el significado de los signos que representan las operaciones matemáticas básicas para después llevar a cabo una generalización a la hora de interpretar los enunciados matemáticos.

Niños que entiende el problema, saben lo que tiene que hacer pero se despistan al calcular: Estos niños entienden el problema, saben lo que tienen que hacer (sumar, restar, multiplicar, dividir), pero olvidan las que se llevan o copian mal los datos al realizar las operaciones. Hay que concienciar al niño de que su problema reside únicamente en este punto, ¿Cómo? Utilizando las autoinstrucciones (paro, miro, decido-qué y cómo, atento, sigo (lo hago), repaso), para reducir la impulsividad. Cuando un niño ha realizado un problema incorrectamente y repasa su ejecución con la ayuda de las autoinstrucciones de Meichenbaum, descubre que ha realizado bien el primer paso (sabe qué debe hacer: paso 1), que sus estrategias para realizar el problema han sido correctas (sabe cómo hacerlo: paso 2), pero ha procedido de forma impulsiva y desatenta (no ha tenido en cuenta que debe estar atento y tener en cuenta todas las posibilidades: paso 3). La estrategia a seguir será: recordar que debe estar muy atento en ese momento del problema. También podemos representar "las llevadas" a través de dibujos y si se le olvida el signo por despiste colorearlo siempre del mismo color.

Niños que suma con los dedos y muy lentamente: Si queremos desarrollar el cálculo mental, debemos hacer que memoricen sumas sencillas, para esto se pueden utilizar distintos juegos. Podemos utilizar un taco de fichas de archivador de color blanco, o confeccionar hojas con sumas simples para luego cronometrar el tiempo que tarda el niño en hacer cada fila. Al repetir el mismo grupo de operaciones todos los días, el niño podrá ver si va reduciendo el tiempo. También podemos utilizar una tarjeta y colocar una sola operación matemática y por el reverso el resultado. Barajar las tarjetas y tratar de asociar esos números con el resultado, de modo que sea rápido para automatizar el cálculo y que se fie de su memoria, dejando de contar con los dedos.

Niños que no saben las tablas de multiplicar: Procederemos a ayudarlos a memorizarlas de corrido utilizando canciones o soniquetes, para luego practicar con el mismo sistema de tarjetas del apartado anterior.